The full numbers from Wednesday’s counts were released this morning by the Secretary of State’s (SoS) office. They’ve driven another nail in the coffin of R-71.
A total of 23,457 signatures have been checks, which is 17% of the total. Overall 3,054 invalid signatures have been found and eliminated, including 68 duplicates, 2,764 individuals not on the voting rolls, 221 signature mismatches, and 69 signatures for which the corresponding signature is missing.
The cumulative error rate is 13.3%, if the signatures with missing signature cards (hereafter “missing”) are thrown out, or 13.0% if the missing signatures are fully counted. As Goldy has explained, the cumulative error rate for the sample is misleadingly low. This is because duplicates are exponentially underrepresented as the sample size goes down.
Given the number of duplicates found in this sample, the best estimate is that is about 1.7% of signatures are duplicates on the petition. That gives an estimated total rejection rate of 14.7% (treating all “missing” signatures as valid). A rejection rate over 12.4% keeps R-71 off the ballot.
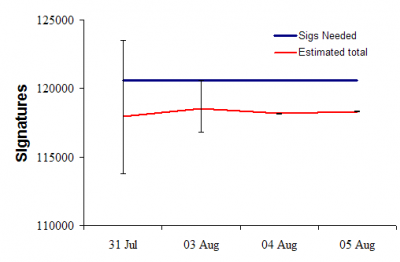
Rather than focus on percentages, we can use the number of good and bad signatures to estimate the expected number of valid signatures. This figure shows the daily estimated number of valid signatures on the petition (red line) and the number of signatures required (blue line) for the measure to make the ballot:
These estimates are conservative because I am assuming all “missing” signatures will be treated as valid. (I’ve changed my methods a bit since yesterday—a journey through the methodological details begins below the fold).
The important things to notice here are:
- The estimates are stable rather than bouncing around from day to day. This means that there is little evidence for non-sampling error. Such errors can arise if batches of petitions showed widely different error rates (more generally, from non-independence among signatures on petitions and in batches of petitions).
- The 95% confidence intervals are now so small that sampling error is no longer relevant. If God plays dice, she clearly doesn’t want R-71 on the ballot.
The trends, so far, indicate that, short of a miracle, this measure will not qualify for the ballot.
At this point, I am going to totally geek-out and discuss methodological stuff. If you’re interested, venture below the fold.
There are three methodological issues in trying to predict the total number of valid signatures based on a smaller sample of signatures.
The first is estimating the total number of duplicates, the second involves actually estimating the number of valid signatures, and the third is finding the sampling error (i.e. the uncertainty that arises because we only sampled some of the signatures).
Estimating the total number of duplicates from a sample: If we assume that there is some constant probability that each person will sign twice (and no more than twice), it means that the percentage of duplicate signature pairs increases with the sample size. Specifically, as the sample size goes up, the number of duplicates goes up nearly (but not quite) as the square of the ratio of total signatures to sampled signatures.
The commonly accepted method for estimating duplicates from a sample was proposed by L.A. Goodman in 1949 (Annals of Mathematical Statistics 20:572-9). Goodman’s method estimates the total number of duplicate pairs (D) in a petition with N signatures from observing d duplicates from a sample of n signatures. The equation is:
The estimate is unbiased under the assumptions stated above.
For example, in yesterday’s data dump, there were d = 68 duplicates found in a sample of n = 23,457 in a petition of N = 137,689 signatures. An estimate of the number of duplicates is 68×137,689×137,688/(23,457×23,456) = 2343.
The estimate of total duplicates could be thrown off if many people sign more than twice. But as of yesterday, nobody had done so.
Estimating valid signatures: This task is slightly indeterminate because it depends on the specifics of how the signatures are examined. There is a difference whether signatures are checked for validity first and only valid signatures are checked for duplication, or whether duplicates are sought first and then validity checked. Of course, there may well be a mixture. To me, it seems like the most logical processing would be to first check if the person is in the voter rolls, then check for duplication, and finally for a mismatch against the signature.
Since I don’t know the exact method the SoS uses, let’s start with the assumption that all invalid signatures are first removed and then the remaining signatures are checked for duplication. Under these assumptions, an unbiased estimate of V valid signatures for a petition, given b invalid signatures in the sample is:
(This estimator, and others that make different signature processing assumptions, are found in MM Whiteside and ME Eakin (2008) The American Statistician 62(1):17-21.)
The logic behind this equation is that we start with N signatures (first term on the right hand side), remove the invalid signatures (second term) and finally remove duplicates from the remaining valid signatures (third term).
Using this estimator with the numbers from yesterday’s count, we estimate 117,807 valid signatures.
I wrote this post yesterday, while sitting around waiting for a data dump . It didn’t come yesterday evening, but it gave me time to derive a hitherto unknown estimator for the number of valid signatures based on a more realistic processing scenario. The scenario is that the SoS office first checks to see if a person is in the voter rolls, then checks to see if that person has already been recorded as signing the petition, and finally checks the signature against the signature on file.
For a petition of N signatures, with a sample of size n, a total of r signatures from people not on the voter rolls, d duplicates, and m signature mismatches, we get this estimator for the total number of valid signatures:
So using yesterday’s totals, the equation gives us an estimated 118,330 valid signatures (assuming the “missing” signatures are all valid). So just by making more realistic assumptions about the processing sequence, the estimated number of valid signatures has increased by about 500. Still, the measure falls well short of the 120,577 needed to make the ballot.
Estimating sampling error. Sampling error arises whenever we use a fraction of signatures to estimate properties of all signatures on a petition. Sampling error is largest for small sample sizes. Once the sample becomes large relative to the number of signatures, sampling error becomes negligible. We are at that point now where sampling error is pretty small.
I’ve not found an explicit formula for the standard error of V (and haven’t derived it for V2). An approximation can be found using simulations. Here is a brief description. For each data dump, I simulated 10,000 petitions being sampled at the observed sample size. For each, I draw a random number of invalid signatures, based on observed invalid signature count, and I draw a random number of duplicates, based on the observed duplicate count and the remaining valid signatures in the sample. [Super geeky technical details: I draw a number of invalid signatures, b’, from a beta-binomial distribution with parameters b and (n – b). Then, I draw a number of duplicates, d’, from a beta binomial distribution with parameters d and (n – b’ – d)]. An estimate of V is then found from the equation above. The average of the 10,000 Vs is the expected number of signatures (V*), and the standard deviation of the Vs is an approximate standard error for V*. In fact, I used the upper and lower 2.5% quantiles of the 10,000 Vs as a 95% confidence interval for V*.
Extensions to V2 are straight-forward. Now we require three draws from a beta binomial distribution because we have broken invalid signatures into three categories (non-registered, duplicates, signature mismatches) to account for processing order.
Yesterday’s data from the SoS office had sampled 23,457 signatures. I computed V2* = 118,330 with a 95% confidence interval of from 118,305 to 118,350. Clearly, this is negligible error since 120,577 valid signatures are needed for R-71 to qualify, and none of the simulated petitions qualified. Look at what happens when the sample size is smaller. Last Friday’s data sampled 5,646 signatures, and V2* = 117,933 with a 95% confidence interval of from 112,348 to 122,059. In the simulations, 13% of the petitions qualified (assuming “missing” signatures all counted).
Last Friday, R-71 had a bit of a chance. The expected number of valid signatures fell short of the threshold, but that could have been bad luck in the sampling. Now, with a larger sample examined, the shortfall is definitely not a function of chance.

Interesting stuff, Daryl.
Just curious though, is this more then the usual number of duplicates on an initiative, and if so, what is the usual percentage for bad signatures on an initiative?
Sampling error was never an issue. These are not random samples. Using the same logic, the “sampling error” on the 1936 poll that forecast Alf Landon beating FDR in a landslide was really small given the 2,000,000 responses.
Montanto,
Just curious though, is this more then the usual number of duplicates on an initiative, and if so, what is the usual percentage for bad signatures on an initiative?”
I believe Goldy has some actual numbers from past initiatives and referenda (I don’t) and will write about it. I discussed this a bit with Goldy yesterday and he suggested the duplication might be low for several reasons.
First, the referendum collection season is much shorter than an initiative season, likely lowering the duplication rate on referenda. Secondly, the chance that a person signs twice might be a function of how many signature drives are going on simultaneously. The more drives the more likely someone forgets exactly which ones he/she has already signed.
Rob @ 2,
Sampling error was never an issue.
Yes…it was for the first couple of days. Now it’s not, unless we get much closer to the threshold number of signatures.
“These are not random samples.”?
In real-life settings (i.e. non-laboratory studies of humans), one is almost never able to attain a true random sample. But if non-sampling error is not apparent, and there is reason to believe the samples are mostly independent, it is very common and acceptable to estimate sampling error to help quantify uncertainty. (And for some types of non-random sampling there are methods of quantifying sampling error that explicitly accounts for the non-independence.)
In this case, there is little evidence of non-sampling error of any magnitude. Furthermore, there are no strong reasons to believe that the signatures are not largely independent with respect to validity.
“Using the same logic, the “sampling error” on the 1936 poll that forecast Alf Landon beating FDR in a landslide was really small given the 2,000,000 responses.”
LOL! You are referring to a single poll from the now-defunct Literary Digest. There was another poll at the same time that got the winner right. But in the 1930, the science of polling was in its infancy. So, your example seems pretty idiotic.
While you’re at it, you might recompute the rate of good sigs the initiative must achieve on the unexamined sigs.
The hill ahead of them gets steeper as they under-achieve on the early legs of the curve.
Or did you do that already. (I confess I did not read closely.)
RonK,
They need to have 100,242 or more valid signatures in the remaining 114,232 signatures. That allows for a maximum rejection rate of 12.25% in the remaining sample to qualify. At the start of the process they needed 12.43% or less.
Gay-hating bastards. May their defeat be ignominious as all hell.
Darryl @ 4, I have to disagree with your use of “sampling error”. (I work with sample statistics for a living.) The sampling error (“margin of error”) can only be applied to random samples (or at the very least samples where we know each member’s probability of falling into the sample). I do agree, however, that this is the real world, not a laboratory, and we don’t have the luxury of a random sample.
But I do have concerns that there is an unintentional bias in how these batches of signatures are being selected. If we define the invalidity rate as non-voters and signatures that don’t match, the first two days had a total invalidity rate of 11.8%. The 3rd and 4th days had a total invalidity rate of 13.6%, for a difference of 1.8%. There is less than a 1% chance that the difference between two random samples of this size is greater than 1.2%.
Another concern is how the projected duplicate rate is declining over the four days: 3.0%, 2.4%, 2.1%, 1.7%. I think there is a geographic bias in how these batches are being selected, which could explain this declining rate. Perhaps, too, some geographic regions have a higher percentage of non-voters who sign referenda than other regions do.
I agree with your bottom line that this referendum is toast (although my champagne is still on ice until it becomes a mathematical certainty). But I disagree with your use of the term “sampling error”.
Rob,
“I have to disagree with your use of “sampling error”. (I work with sample statistics for a living.)”
So do I. In fact, I teach graduate-level applied social science statistics at the University of Washington.
“The sampling error (”margin of error”) can only be applied to random samples (or at the very least samples where we know each member’s probability of falling into the sample).”
This isn’t really true. For example, in using finite mixture models we must estimate the probability of membership in subgroups, and yet can talk rationally about sampling error.
“I do agree, however, that this is the real world, not a laboratory, and we don’t have the luxury of a random sample.”
Ok.
“But I do have concerns that there is an unintentional bias in how these batches of signatures are being selected.”
As I have suggested, there may be, but we cannot see much evidence for it right now.
“If we define the invalidity rate as non-voters and signatures that don’t match, the first two days had a total invalidity rate of 11.8%. The 3rd and 4th days had a total invalidity rate of 13.6%, for a difference of 1.8%. There is less than a 1% chance that the difference between two random samples of this size is greater than 1.2%.”
As you can see from the graph above, 13.6% is well within the 95% confidence intervals for the first two days.
“Another concern is how the projected duplicate rate is declining over the four days: 3.0%, 2.4%, 2.1%, 1.7%.”
I haven’t explicitly tallied the standard errors for the cumulative duplicate rates, so I cannot say, offhand, whether they differ significantly from each other. But keep in mind that the sampling error is much larger than binomial sampling error. This is because we have a doubly-stochastic process. There is ordinary binomial error in the projection, but the estimate of the probability of duplication itself has sampling error (hence drawing from a beta binomial distribution that accounts for both sources of sampling error).
“I think there is a geographic bias in how these batches are being selected, which could explain this declining rate. Perhaps, too, some geographic regions have a higher percentage of non-voters who sign referenda than other regions do.”
Could be. But we don’t see it in the projections of total valid signatures.
‘But I disagree with your use of the term “sampling error”.’
I’m not sure what you are getting at. Sampling error exists whenever a sample is taken–whether a random sample or not. Perhaps you are quibbling with the way I am estimating it (i.e. believe it is biased)? Either way I think we can both agree that the sample size after day 2 is too large for sampling error to be much of an issue.
Aah, nothing more satisfying than a good geekout!
Thanks Darryl for laying out your thesis. You won’t be surprised to hear me echo Rob, however. Your analysis is based on the assumption that the samples so far have been representative of the entire 137,689 pool of raw signatures. We won’t know whether that’s the case until we’ve seen them. It wouldn’t surprise me, for example, for some batches of petitions to have been collected in a closed, controlled locations (church, KoC meeting hall) where the organizers were very careful to have people fill out voter registration cards at the same time as needed, and therefore to have exceedingly low Not Found rates. Larry Stickney is a bumbling idiot in so many ways, but he has been working the conservative voter registration picket for years and could conceivably managed this level of organization in some palces. These are the real world considerations which make me keep my Mt Dew capped tight and my butt in the WAFST.org volunteer chair until, as Rob said, we know that it is mathematically impossible for this flaming load of bigot crap to qualify for the ballot.
Lurleen,
“Thanks Darryl for laying out your thesis. You won’t be surprised to hear me echo Rob, however. Your analysis is based on the assumption that the samples so far have been representative of the entire 137,689 pool of raw signatures.”
It is.
“We won’t know whether that’s the case until we’ve seen them.”
True, but it won’t be any fun projecting the outcome at that point….
“It wouldn’t surprise me, for example, for some batches of petitions to have been collected in a closed, controlled locations (church, KoC meeting hall) where the organizers were very careful to have people fill out voter registration cards at the same time as needed, and therefore to have exceedingly low Not Found rates.”
Another possibility are petition sheets from churches near Oregon or Idaho, where there may be more out-of-state signatures. Even so, Ammons post today mentions 20 signature checkers. I think it is very likely they are working out of different batches of ballots.
good point about the 20 different signature checkers. however, there are still bundles of unchecked petitions amounting to over 110,000 raw signatures that none of those 20 diligent workers have had the chance to look at yet. my scenario is still possible, unfortunately.
idaho and oregon – i suppose we won’t know how prevalent sigs from those folks were until the sos releases the petitions to the public. but i did hear from an organizer that there were “a lot” of oregon signers. but what she considered a lot she didn’t say, and whether this was a systemic problem or a local one as you surmise, she didn’t mention.
oh, and you’re right of course that it isn’t any fun to project the outcome once you already know it. but it also isn’t any fun to watch people roll the dice with something so serious as civil rights repeal on the ballot. if this were a referendum about new toothpick regulations, i’d be right there with you in the joy of the moment.
Darryl @ 9, this truly is a geekout!
I think what we have is the possibility of “coverage error” in these batches of samples. If they are geographically clustered, then signatures from another geographic area have zero percent chance of being in that batch. Sort of like the 1936 poll that used telephone books and automobile registrations as the sample frame. The coverage error there was that Democrats effectively had zero chance of falling in that sample!
Also, if we split the batches into two 2-day samples of about 11,000 each and pretend they are random samples from the same population, the odds are very much against these samples differing in their validity rate by as much as 1.8%. (Isn’t the 95% confidence interval about 0.6%? for each one?) So, I do think these batches have some bias in them.
But we really are debating about the number of angels on the head of a pin. Any bias so far in these batches is immaterial in terms of whether this referendum has enough valid signatures. Barring a major shift in the remaining signatures, R-71 is toast.
Rob,
“this truly is a geekout!”
Indeed! :-)
“I think what we have is the possibility of “coverage error” in these batches of samples. If they are geographically clustered, then signatures from another geographic area have zero percent chance of being in that batch. Sort of like the 1936 poll that used telephone books and automobile registrations as the sample frame. The coverage error there was that Democrats effectively had zero chance of falling in that sample!”
But here we have a much smaller population and we are now at a fairly large sample from the population. The latest data dump is about 20%. Also, with 20 counters, I am less concerned about a chronological trend (especially given the results so far.)
“Also, if we split the batches into two 2-day samples of about 11,000 each and pretend they are random samples from the same population, the odds are very much against these samples differing in their validity rate by as much as 1.8%. (Isn’t the 95% confidence interval about 0.6%? for each one?) So, I do think these batches have some bias in them.”
On day two, the 95% CI went from 116,503 120,288 which is 84.6% to 87.4%, or 1.4% each direction. The next three days, the mean estimates are 118167, 118330, 118184.
For days 3, 4 and 5 the 95% CIs swing 70, 45, and 35 signatures around the mean respectively, whereas we are seeing swings as large as +/- 150. Therefore we see some variability in excess of sampling error. But, it looks pretty ignorable. If the V2 estimator for day 3 comes within +/-150 of the final number of valid signatures, I’ll be mighty pleased.
“But we really are debating about the number of angels on the head of a pin. Any bias so far in these batches is immaterial in terms of whether this referendum has enough valid signatures. Barring a major shift in the remaining signatures, R-71 is toast.”
Agreed!
Something tells me, perhaps experience, that this level of conversation wouldn’t be happening over at SP…
Makes me glad that when I signed this petition up in Mt. Vernon a while back, I signed it “Martin Buber,” of Wickersham. It’s my new petition tactic: sign ’em all but sign the ones I hate w/the name of a dead theologian.
BA @ 16,
“Something tells me, perhaps experience, that this level of conversation wouldn’t be happening over at SP…”
You’ve got to be kidding. I once saw on SP a brilliantly quantitative discussion thread on whether Democrats or Republicans were better at lighting their farts….
OK, but did they have their math right?