HorsesAss.Org

Poll analysis FAQ

This page describes the simulation analyses that appear on HorsesAss.

What are these simulations all about?

Four types of Monte Carlo-based simulation analyses are done here.

  1. Local and statewide elections and ballot measures.
  2. Presidential election based on state head-to-head polls
  3. Senatorial elections based on state head-to-head polls
  4. Gubernatorial elections based on state head-to-head polls

Essentially, one of us (Darryl) has a hobby of collect polls and using them to simulate election results. Darryl has been doing local elections for many years on HA. The more intensive effort to analyze presidential elections began in October 2007 (at the now defunct HominidViews) for the 2008 presidential election. State head-to-head poll were systematically collected and used to assess the state of the election—the score, if you will. Later he added the 2008 senatorial and gubernatorial elections. This FAQ mostly discusses the presidential election, although the methods are applicable for other simulation analyses presented here.

How are you doing the electoral college analyses?

The analyses are Monte Carlo simulations of the Electoral College outcome based on state head-to-head polling data. The results are driven by poll results (or, when there are no poll results for presidential elections, the average of the three previous presidential elections). Essentially, we simulate a large number of elections (typically 100,000) for all states based on recent polling data. Presidential elections also include D.C., and Nebraska and Maine districts based according to the rules of the electoral college. The winner for each state is determined randomly according to the proportions of people selecting each candidate in recent polls. After all state elections have been simulated, we tally control of the Senate (Senate elections) or the number of Electoral College votes for each candidate (presidential elections). Details of the methods follow.

What polling data do you use?

For the presidential race, we collect state polls in which the top Democrat is matched-up, head-to-head, with one or more likely Republican challenger. For the 2008 election season we did multiple match-ups: Obama v. McCain, Obama v. Romney, Obama v. Huckabee, Clinton v. McCain, Clinton v. Romney, …, etc. In 2012 the match-ups were limited to Obama against several Republican front-runners until Romney was nominated. For 2016, we had numerous parings. For 2020, there was an incumbent (Trump) and the Democratic nominee was apparent by the Spring.

For the senatorial and gubernatorial elections we do the same thing using data for each state in which there is an election.

Where do your polling data come from?

Several places. We find polls from the web sites of well-known polling firms. However, if there is sufficient information, a secondary source (e.g. news summary of a poll) can be acceptable. The most common polling firms that release head-to-head polls are SurveyUSA, Rassmussen and Quinnipiac. But there are many, many more polls and polling companies. Frequently, we are made aware of a poll through a polling aggregation site like Atlas of US elections, Pollster.com, fivethirtyeight.com or Real Clear Politics, but we try to find (and link to) original poll reports.

How do you select which polls to include?

To be considered acceptable, each poll must come from a reputable pollster and must included the following information:

  1. The name of the poll or polling firm
  2. The inclusive dates on which the poll was taken
  3. The state in which the poll was taken
  4. The number of individuals polleda
  5. The counts of or percentage of individuals supporting each candidate

aMost reputable polls include the number of individuals sampled. Occasionally a poll does not include that number. When a 95% margin of error (MOE) is provided, an estimate of the number of sampled individuals can be found as (0.98/MOE)2. This is based on the standard error of a binomial distribution and, as is commonly done by pollsters, assuming the true proportion for each candidate is 0.5. This is not ideal…numbers are preferred.

We used to exclude internet-based polls, because they were largely garbage. More recently, legitimate polling firms have developed methods to approximate a random sample using internet-based polls. In recent election cycles, we will include such polls if the methods seem legitimate. Polls from discredited pollsters (remember Research 2000 and Strategic Vision?) are always excluded. We also ignore polls released by party organizations or candidates. The problem is that such polls are released strategically, so that including them biases results. The rule of thumb is this: if the release of a poll seems contingent on which candidate is ahead, by how much a candidate leads or lags, or by how close the race is, this poll is not suitable for inclusion.

Some polls include results for multiple respondent categories. For example, “all adults,” a subset of “registered voters,” and a subset of “likely voters.” We always take take the sample most likely to represent voters. So between “all adults” and “registered voters,” we take the latter. When results are given for both “registered voters” or “likely voters” we take the “likely voter” results.

Do you include push polls?

No. A push polls is a marketing tool, not a poll. In any case, results of push polls are rarely, if ever, published.

Do your simulations include all polls in each state?

No. We use recent polls whenever possible. For example, if there are two polls in the last three weeks for Missouri and four older polls, only the two “recent” polls are included in the simulations. How far back to go is an arbitrary decision that is, to a certain extent, driven by the number of polls being released.

Early in the election season “recent” means polls that are up to one month old—that is, we used a one month “current poll” window. Then, beginning in mid- to late-summer of an election year polls start to pour in fast and furiously, and the “current poll” window is reduced to three weeks. Perhaps by October, it will be reduced to two weeks. A 10 day window is used around mid- to late-October. A final reduction to a one week window occurs about a week before the election.

What if there are no polls that have been conducted in the “current poll” window?

In that case, we use the single most recent poll taken, even if it was taken some months ago.

What if there are no polls whatsoever taken in the state?

In that case, that state always goes the way it did in the past.

We use the average of the the three recent election results for presidential elections. States that went for Romney, Trump and Trump are always assumed to go for the Republican candidate. State that went for Obama, Clinton and Biden are assumed to go for the Democratic candidate. When there are mixed results we average the percentages based on party and give that state’s electors to the “winning” party.

For senatorial and gubernatorial elections, we simply keep the party of the current Senator or Governor, respectively.

Why use past election results for states lacking any polls?

This seems like the best strategy given an absence of polls. The states with no polling are those that the media and polling firms believe are highly predictable—therefore there is no reason to pay good money to conduct a poll. They’re probably right. For example, Hawaii is, almost certainly, not going to go for the Republican candidate in a presidential election, so polling in Hawaii is unlikely—at least until we get much closer to the election.

Of course, as the election season goes on, there will be fewer and fewer un-polled states. In 2004, all 50 states plus D.C. were eventually polled, but there was only a single poll in some cases (like D.C.). In 2008, there were polls conducted in every state & D.C. Again, there was only one poll for D.C.

How can I see the polls being used?

From the map, click on a state to jump to the results table. From there, click on the number in the “# polls” column, and you will be taken to a list of polls.

What about races with 3rd party candidates?

When a poll gives a two-way race (e.g. Clinton vs. Trump) as well as a three- or four-way race (e.g. Clinton vs. Trump vs. Johnson vs. Stein), we take the results of the 3-way or 4-way race. The third party votes are rolled up into an “other” category and not included in the analysis, but it does capture the effect of how 3rd party votes reduce the number of votes, as well as changes to the relative proportion of votes for the Democratic and Republican candidates.

How are the simulations done?

For each simulation, an election is “held” in each state (plus D.C. plus districts for Nebraska and Maine in presidential elections) using “current” polls. For the presidential analyses, state results are then combined as would happen in the electoral college—winner takes all in 48 states plus D.C., and by the special rules for Nebraska and Maine.

As an example, in Feb 2008, there was a single poll conducted in Maryland for the Obama–McCain match-up. A Rasmussen poll was conducted on 2 Jan 2008 and surveyed 500 voters, finding that 42% support McCain, 48% support Obama and 10% were either undecided or supported someone else. (This poll was “old” because it was more than a month old, but it was the most current poll at the time, so it was the best information available.) Here are the steps involved using data from the 2008 election:

  1. The number of people who voted for each candidate are found. Some polling companies (like SurveyUSA) make the actual numbers available. Otherwise the numbers are computed: 500*0.48 gives 240 votes for Obama and 500*0.42 gives 210 McCain supporters in the poll. There were 240 + 210 = 450 decided voters.
  2. The computer normalizes the percentage who voted for each candidate. For Obama it was 240/450 = 53.33%, and was 46.67% for McCain. “Normalized” means that the percentage for Obama and McCain summed to 1.0.
  3. The estimated probability of a voter voting for Obama in Maryland in Jan was p= 0.533. But since p itself is estimated from a sample, p is more properly described as a distribution of possible Obama preferences. That is, we really have a distribution of ps.

    4. Thus, in each simulation for each poll, the computer randomly draws a value from the distribution of ps (let’s call it p’). So for the current simulation we might draw the value p’ = 0.527. Technical details: We draw p’ from a beta distribution with parameters (Dvotes + 1) and (Rvotes + 1). So, in this example we draw randomly from a beta distribution with parameters 241 & 211. This corresponds to a binomial distribution with a uniform (uninformative) prior distribution p.

  4. Now, we simulate 450 voters, who each have a p’ (here, a 52.7%) probability of voting for Obama and 1 – p’ probability of voting for McCain. How is this done? The easy way is to draw a uniform random number between 0 and 1. If the number is less than 0.527 then the vote goes to Obama, otherwise it is a vote for McCain. The process is repeated 450 times. Technical details: In practice we use a much faster method that yields identical results. A number of votes for the candidate is drawn from a binomial quantile function with a uniform random number as its argument and parameters N and p’ (here, 450 and 0.527).

When there are multiple current polls this process is repeated for each poll in each state and the number of votes for each candidate tallied.

How are you incorporating undecided voters in your analysis?

Undecided voters are ignored. In absence of any information, the method assumes that the undecided fraction will break as the decided sample breaks.

Maine and Nebraska use a different method of assigning electoral college votes. Shouldn’t you treat them differently?

All states but Maine and Nebraska use winner-take-all for electoral votes. For Maine’s two and Nebraska’s three districts, one elector is given to the candidate who wins the district’s popular vote. The other two electors go to the candidate who wins the state’s popular vote.

We ignored this little detail in the 2008 election season because neither state had ever split its electoral votes among candidates in the past. But one district in Nebraska did split from the statewide vote in 2008. As a consequence, our final mean electoral outcome was off by a single electoral vote. Doh! So now we use polling information at the congressional district level for Maine and Nebraska. Essentially, the districts are treated as states.

Are you doing your analyses to favor a particular candidate or party?

These election analyses are done as objectively as we can possibly make them. The results are driven by the numbers found in hundreds of polls. A few arbitrary decisions, like “current poll” window size, are necessary to do these analyses. These are all well documented and are not intended to favor any party or candidate.

Are you trying to predict the result of the election?

No. The analyses make no projections to election day, (except the one we run on election day). Rather, we view this as showing what the state head-to-head polls indicate would happen if the election had been held today.

Let’s use a sports metaphor. During a basketball game, the current score does not always predict the winner. Rather, it provides information on the past and current performance of each team. We get some indication of the eventual winner, but only as the end of the game approaches or when point difference gets very large. Still, do you think it would be acceptable to not give the score until after the game is over? Probably not. Fans want to see the score right from the start.

Likewise in an election contest, these analyses serve as a score for each “team.” I fully expect the score and the point spread to change as the game goes on, but I want to know who is in the lead and by how much at every point of the game.

Aren’t these exercises futile early in the election season when the political parties are focused on the primary instead of messaging?

No. Again, from the sports metaphor, would it be acceptable to hide the score for the first half of a basketball game? A team’s strategy, spending, name recognition and numerous other things may change throughout the game, but the strategy adopted for the second half will be based on the current “score.”

In fact, the ebbs and flows over time—particularly with respect to events and media coverage—are fascinating. For example, Giuliani’s 2008 fall from grace in the polls after LoverGate, and in the absence of any showing in IA and NH was nothing short of stunning. Likewise, Romney’s best polling performance happened just after a poor first debate performance by Obama. These sorts of things can be quite interesting.

Why not use national head-to-head polls instead?

National polls have the advantage of being current—that is, people express their support for each candidate all at the same time. The state head-to-head polls suffer because some polls are older (or missing altogether), and public opinion may have changed since the older polls were taken. But the national head-to-head polls have a big disadvantage. Most importantly, they predict the outcome of a national popular vote. We don’t elect our presidents by popular vote. As we learned in 2000 and 2016, the national popular vote doesn’t always give the same election outcome as the Electoral College vote.

How are you incorporating the margin of error of each poll in your analysis?

The margin of error is inherently incorporated into the analyses. This is done by simulating elections in each state that include the number of polled individuals, and drawing a new value of p’ (described above) for each poll every simulated election.

What is the distribution of electoral votes?

The “distribution of electoral votes” graph look like this (from the 2008 election):

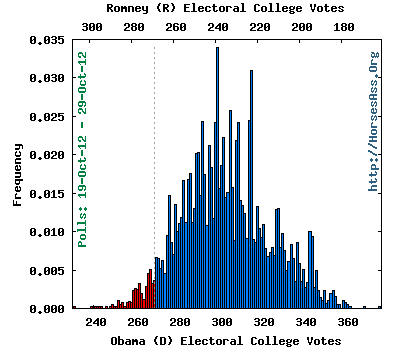
To produce this graph, the computer saves the electoral vote from each of the (typically, 100,000) simulated elections. Then, the relative frequency (on the y-axis) of each possible electoral vote outcome (x-axis) is plotted. The graph can tell you several things:

  1. The highest bar is the most likely outcome for an election—this is the mode of the distribution. In this example from Oct 2012, the mode is 299 electoral votes, and there is a 3.39% probability of this outcome (in an election held then). The next highest bar is at 315 electoral votes with a 3.09% probability.
  2. The vertical dashed line is simply a marker for 269 votes—which reflects a tie in the Electoral College. The blue bars to the right of the center line are wins for the Democrat and the red bars to the left are wins for the Republican
  3. If you squint a bit you can estimate where the graph would balance on a fulcrum. That would be your estimate of the mean (or average or expected electoral vote total.
  4. The point on the x-axis were half of the bars fall above and half fall below is the median electoral vote.
  5. The spread of the distribution is an indication of how variable the outcomes are.
  6. The raggedness of the bars reflects the differing numbers of votes per state with an Electoral College system. With 100,000 simulations, we would expect a pretty smooth distribution if a popular vote was being simulated. Not necessarily so with an electoral college system because states are won wholesale.

How are the trend graphs produced?

The trend graphs look like this:

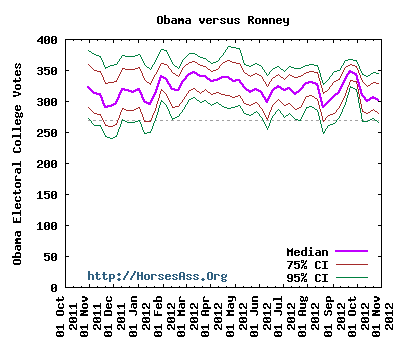
The graph results from simulations done over time. This graph was created by simulating weekly elections over a twelve month period. Basically, this comes from a series of 100,000 simulated elections for every week from October 2011 through October 2012.

The graph shows the median electoral vote count (purple line) for Obama. The blue lines enclose the central 75% mass of Obama’s electoral vote counts, and the green line enclose 95% of Obama’s electoral vote count. One thing this shows is that Romney never held the lead during the 2012 election season through October. Through 2012, Romney briefly had about a 25% chance of winning an election held at the time.

What do the colors mean?

The “party colors” are used at several intensities to convey information in four places:

  1. On the map
  2. On the state results summary table
  3. On the poll list
  4. On lists of polls for an individual state

For the first two cases (map and results table), the colors are coded according to the probability that the Democrat wins based on the actual results of the simulation analysis:

Color From To
100% 99.999%
99.999% 90%
90% 60%
60% 50%
Exactly 50%
50% 40%
40% 10%
10% 0.001%
0% 0.001

The poll results table and state poll lists are different, because the simulation results are not saved by poll (and the state poll lists don’t involve simulations at all). Instead the colors reflect the result of a t-test of the hypothesis that the Democratic results is greater than the Republican results. Technically, we compute

T-test equation

where d is the normalized Democratic proportion, r is the normalized Republican proportion and n is the number of individuals who responded for either the Democratic or Republican candidate. The T statistic is compared to a Student’s t distribution to decide the probability of the Democrat winning given the observed poll results. The same cut-offs as in the table above are used.

What is that distorted map thing?

This is a cartogram. Here is one from the 2012 presidential election:

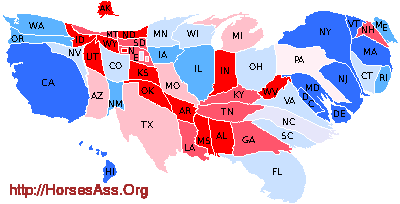
The cartogram scales the area of each state according to its electoral vote total. Thus, Alaska is scaled to the same size as Washington D.C.—both have three votes in the Electoral College. The cumulative area covered by each color on the cartogram is an honest representation of the proportion of electoral votes that would be expected if a general election were held.

For more information on cartograms, check out Mark Newman’s web page or Victor L. Vescovo’s book The Atlas of World Statistics (2006, published by Caladan Press).

Note that the cartogram for the electoral college changed between 2008 and 2012. This is because the U.S. census changed the allocation of Representatives among the states, which changed the number electoral college electors from some states. They will change again for the 2024 election.

Why do you assign electoral college ties to the Republican candidate?

In the event of a 269–269 tie in the Electoral College, the selection of the next President and Vice President is specified by the 12th Amendment of the U.S. Constitution. The new House of Representatives would vote (using an unorthodox single-vote-per-state method) for the President and the Senate would select the Vice President. At this point, it looks like the Republican candidate would get the necessary 26 votes for President should neither candidate get 270 electoral votes.

Can’t Bring Yourself to Type the Word “Ass”?

Eager to share our brilliant political commentary and blunt media criticism, but too genteel to link to horsesass.org? Well, good news, ladies: we also answer to HASeattle.com, because, you know, whatever. You're welcome!

Follow Goldy

[iire_social_icons]

HA Commenting Policy

It may be hard to believe from the vile nature of the threads, but yes, we have a commenting policy. Comments containing libel, copyright violations, spam, blatant sock puppetry, and deliberate off-topic trolling are all strictly prohibited, and may be deleted on an entirely arbitrary, sporadic, and selective basis. And repeat offenders may be banned! This is my blog. Life isn’t fair.